Wzór na czas, prędkość i dystans: klasa 4. Jak znaleźć czas, znając prędkość i dystans? Jak znaleźć prędkość, jeśli znany jest czas i odległość? Jak znaleźć odległość, jeśli znany jest czas i prędkość? Wykres zależności prędkości ciała od czasu

Jak rozwiązywać problemy ruchowe? Wzór na zależność między prędkością, czasem i odległością. Zadania i rozwiązania.

Wzór na zależność czasu, prędkości i odległości dla klasy czwartej: jak wskazuje się prędkość, czas, odległość?

Ludzie, zwierzęta lub maszyny mogą poruszać się z określoną prędkością. Mogą iść określoną drogą w określonym czasie. Na przykład: dzisiaj możesz dotrzeć do szkoły w pół godziny. Idziesz z określoną prędkością i pokonujesz 1000 metrów w 30 minut. W matematyce pokonana droga oznaczona jest literąS. Prędkość jest oznaczona literą v. A czas przebycia drogi oznaczony jest literą t.

• Ścieżka —S
• Prędkość — v
• Czas —t

Jeśli spóźnisz się do szkoły, może to samo przejść w ciągu 20 minut, zwiększając prędkość. Oznacza to, że tę samą ścieżkę można pokonać w różnym czasie iz różnymi prędkościami.

Jak czas podróży zależy od prędkości?

Im większa prędkość, tym szybciej pokonany dystans. A im mniejsza prędkość, tym dłużej zajmie podróż.

​​​​

Jak znaleźć czas znając prędkość i dystans?

Aby znaleźć czas potrzebny na pokonanie dystansu, musisz znać odległość i prędkość. Jeśli podzielisz odległość przez prędkość, poznasz czas. Przykład takiego zadania:

Zadanie o Zając. Zając uciekł od Wilka z prędkością 1 kilometra na minutę. Pobiegł 3 kilometry do swojej dziury. Po jakimś czasie Hare pobiegł do dziury?

Jak łatwo jest rozwiązywać problemy ruchu, w których trzeba znaleźć odległość, czas lub prędkość?

1. Przeczytaj uważnie problem i ustal, co wiadomo z jego stanu.
2. Zapisz te dane w wersji roboczej.
3. Napisz również, co jest nieznane i co można znaleźć
4. Użyj wzoru na problemy z odległością, czasem i prędkością
5. Wprowadź znane dane we wzorze i rozwiąż zadanie

Rozwiązanie problemu o Zając i Wilku.

• Ze stanu problemu ustalamy, że znamy prędkość i odległość.
• Na podstawie stanu problemu ustalamy również, ile czasu zajęło zającemu dobiec do dziury.

Dane te zapisujemy w szkicu np.:

Odległość do dołka — 3 kilometry

Prędkość zająca — 1 kilometr w 1 minutę

Czas jest nieznany

Teraz zapiszmy to samo symbolami matematycznymi:

S— 3 kilometry

V — 1 km/min

t—?

Przypominamy i zapisujemy wzór na znalezienie czasu w zeszycie:

t = S: v

Teraz zapisujemy rozwiązanie problemu w liczbach:

t = 3: 1 = 3 minuty

Jak znaleźć prędkość, jeśli znany jest czas i odległość?

Aby znaleźć prędkość, jeśli czas i odległość są znane, odległość należy podzielić przez czas. Przykład takiego zadania:

Zając uciekł przed Wilkiem i pobiegł 3 kilometry do swojej nory. Ten dystans pokonał w 3 minuty. Jak szybko biegał Zając?

Rozwiązanie problemu ruchu:

1. W szkicu piszemy, że znamy odległość i czas.
2. Z warunku problemu określamy, że musimy znaleźć prędkość
3. Przypominamy sobie wzór na znalezienie prędkości.

Wzory rozwiązywania takich problemów pokazano na poniższym obrazku.

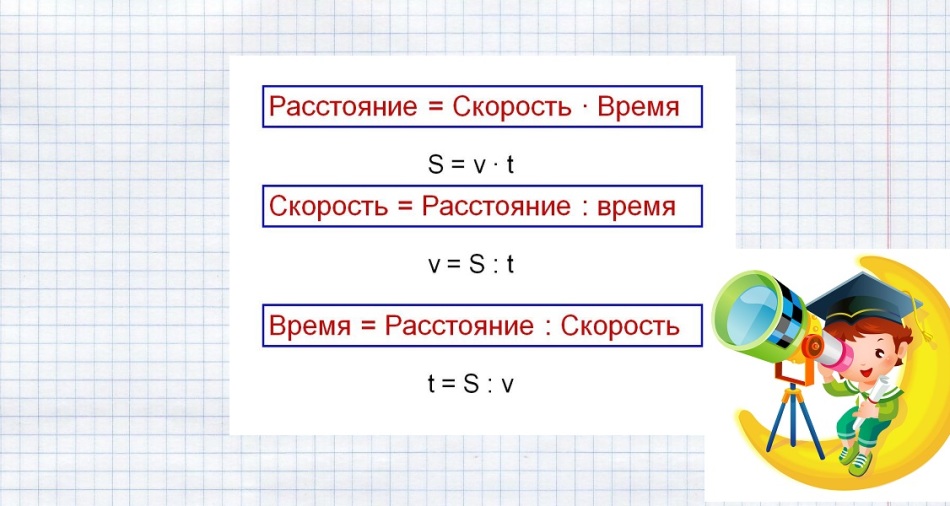
Zastąp znane dane i rozwiąż zadanie:

Odległość do dziury wynosi 3 kilometry

Czas dotarcia do dziury wyniósł 3 minuty

Prędkość jest nieznana

Zapiszmy te znane dane w symbolach matematycznych

S— 3 kilometry

t— 3 minuty

v —?

Piszemy wzór na znalezienie prędkości

v = S: t

Teraz zapisujemy rozwiązanie problemu w liczbach:

v = 3: 3 = 1 km/min

Jak obliczyć odległość, jeśli czas i prędkość są znane?

Aby znaleźć odległość, jeśli czas i prędkość są znane, pomnóż przez prędkość. Przykład takiego zadania:

Zając uciekł od Wilka z prędkością 1 kilometra w ciągu 1 minuty. Bieganie do dziury zajęło mu trzy minuty. Jak daleko uciekł Zając?

Rozwiązanie problemu: W szkicu zapisujemy to, co wiemy ze stanu zadania:

Prędkość Zająca wynosi 1 kilometr za 1 minutę

Czas dobiegł do dziury - 3 minuty

Dystans - nieznany

Zapiszmy teraz to samo symbolami matematycznymi:

v — 1 km/min

t— 3 minuty

S —?

Przypominamy wzór na znalezienie odległości:

S = v ⋅ t

Teraz zapisujemy rozwiązanie problemu w liczbach:

S = 3 ⋅ 1 = 3 km

Jak nauczyć się rozwiązywać bardziej złożone zadania?

Aby nauczyć się rozwiązywać bardziej złożone zadania, musisz zrozumieć, jak rozwiązywać proste, pamiętaj, które znaki oznaczają odległość, prędkość i czas. Jeśli nie pamiętasz wzorów matematycznych, zapisz je na kartce i zawsze miej pod ręką podczas rozwiązywania problemów. Rozwiązuj z dzieckiem proste zadania, które możesz wymyślić w podróży, na przykład podczas spaceru.

Jednostki miary

​​

Rozwiązując problemy dotyczące prędkości, czasu i odległości często popełniają błąd, ponieważ zapominają przeliczyć jednostki miary.

WAŻNE: Jednostki miary mogą być dowolne, ale jeśli w tym samym zadaniu występują różne jednostki miary, przekształć je na takie same. Na przykład, jeśli prędkość jest mierzona w kilometrach na minutę, odległość należy podać w kilometrach, a czas w minutach.

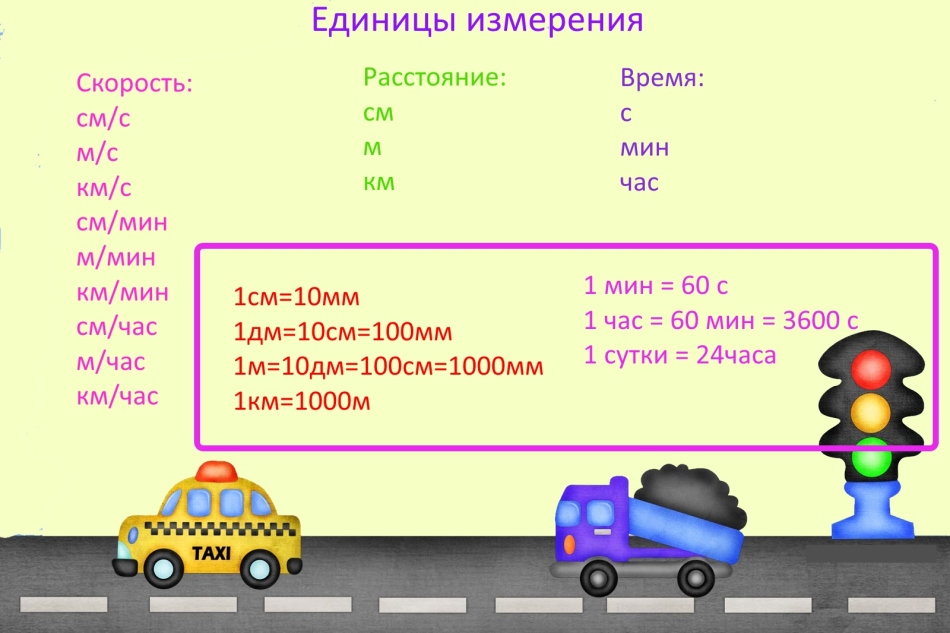
Dla ciekawskich : Ogólnie przyjęty system miar nazywa się metrycznym, ale nie zawsze tak było, aw starożytnej Rosji używano innych jednostek miary.

Problem Boa : Słoń i małpa zmierzyli długość boa w krokach. Podeszli do siebie. Prędkość małpy wynosiła 60 cm na sekundę, a słonia 20 cm na sekundę. Na pomiar poświęcili 5 sekund. Jaka jest długość boa? (rozwiązanie pod zdjęciem)

<> Rozwiązanie:

Na podstawie stanu problemu ustalamy, że znamy prędkość małpy i słoniątka oraz czas potrzebny do zmierzenia długości boa.

Zapiszmy te dane:

Prędkość małpy to 60 cm/s

Prędkość słoniątka wynosi 20 cm/s

Czas — 5 sekund

Odległość nieznana

Zapiszmy te dane symbolami matematycznymi:

v1 — 60 cm/s

v2 — 20 cm/s

t — 5 sekund

S —?

Zapiszmy wzór na odległość, jeśli znana jest prędkość i czas:

S = v ⋅ t

Policzmy odległość jaką przebyła małpa:

S1 = 60 ⋅ 5 = 300 cm

Teraz policzmy, jak daleko przeszło słoniątko:

S2 = 20 ⋅ 5 = 100 cm

Sumujemy odległość przebytą przez małpę i odległość przebytą przez słoniątko:

S = S1 + S2 = 300 + 100 = 400 cm

Wykres zależności prędkości ciała od czasu: zdjęcie

Odległość pokryty z różnymi prędkościami jest pokryty w różnym czasie. Im wyższa prędkość, tym mniej czasu zajmuje ruch.

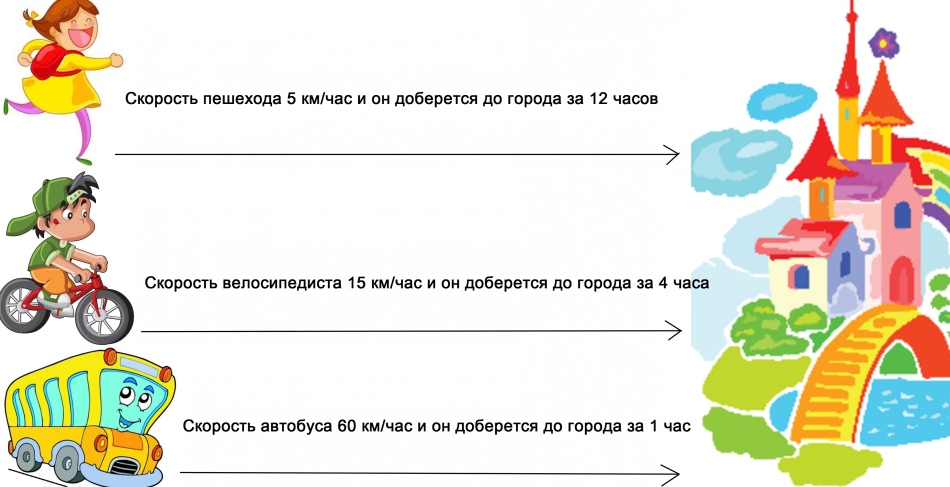
Tabela 4 klasa: prędkość, czas, odległość

Nr	Prędkość (km/h)	Czas (godzina)	Dystans (km)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Możesz fantazjować i wymyślać zadania dla stół sam. Poniżej znajdują się nasze opcje warunków zadań:

1. Mama wysłała Babci Czerwonego Kapturka. Dziewczyna była ciągle rozkojarzona i szła przez las powoli, z prędkością 5 km/h. Po drodze spędziła 2 godziny. Jak daleko w tym czasie przeszedł Czerwony Kapturek?
2. Listonosz Pechkin przewoził na rowerze paczkę z prędkością 12 km/h. Wie, że odległość między jego domem a domem wujka Fedora wynosi 12 km. Pomóż Pechkinowi obliczyć, ile czasu zajmie podróż?
3. Papa Ksyusha kupił samochód i postanowił zabrać rodzinę nad morze. Samochód jechał z prędkością 60 km/h, a na drodze spędziliśmy 4 godziny. Jaka jest odległość między domem Ksyushy a wybrzeżem morskim?
4. Kaczki zebrały się w klin i poleciały w ciepłe rejony. Ptaki machały skrzydłami niestrudzenie przez 3 godziny i pokonały w tym czasie 300 km. Jaka była prędkość ptaków?
5. Samolot AN-2 leci z prędkością 220 km/h. Wystartował z Moskwy i leci do Niżnego Nowogrodu, odległość między tymi dwoma miastami to 440 km. Jak długo samolot będzie w drodze?

Odpowiedzi na zadane problemy można znaleźć w poniższej tabeli:

Nr	Prędkość (km/h)	Czas (godziny)	Dystans (km)
) 1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Przykłady rozwiązywania problemów prędkości, czasu, odległości dla czwartej klasy

Jeśli w jednym zadaniu występuje kilka poruszających się obiektów, musisz nauczyć dziecko rozważania ruchu tych obiektów osobno, a dopiero potem razem. Przykład takiego zadania:

Dwóch przyjaciół Vadyk i Tema postanowiło wybrać się na spacer i wyszło ze swoich domów, aby się spotkać. Vadyk jechał na rowerze, a Tema szedł. Vadyk jechał z prędkością 10 km/h, a Tema z prędkością 5 km/h. Godzinę później spotkali się. Jaka jest odległość między domami Vadyka i Temy?

Problem ten można rozwiązać za pomocą wzoru na zależność odległości od prędkości i czasu.

S = v ⋅ t

Dystans pokonany przez Vadyka na rowerze będzie równy jego prędkości pomnożonej przez czas w tranzycie.

S = 10 ⋅ 1 = 10 kilometrów

Odległość przebyta przez Badanego oblicza się podobnie:

S = v ⋅ t

Podstawić wartości cyfrowe jego prędkości i czasu do wzoru

S = 5 ⋅ 1 = 5 kilometrów

Dystans przebyty przez Vadyka należy dodać do dystansu przebytego przez Tema.

10 + 5 = 15 kilometrów

Jak nauczyć się rozwiązywać złożone problemy wymagające logicznego myślenia?

Aby rozwijać logiczne myślenie dziecka, należy rozwiązywać z niego proste, a potem złożone zadania logiczne. Zadania te mogą składać się z kilku etapów. Możesz przejść z jednego etapu do drugiego tylko wtedy, gdy poprzedni jest rozwiązany. Przykład takiego zadania:

Anton jechał na rowerze z prędkością 12 km/h, a Lisa jechała na hulajnodze z prędkością 2 razy mniejszą niż Anton, a Denis szedł z prędkością 2 razy mniejszą niż Lisa. Jaka jest prędkość Denisa?

Aby rozwiązać ten problem, musisz najpierw znać szybkość Lisy, a dopiero potem szybkość Denisa.

Dwóch rowerzystów wyjechało z różnych miast, aby się spotkać. Jeden z nich spieszył się i biegł z prędkością 12 km/h, a drugi jechał spokojnie z prędkością 8 km/h. Odległość między miastami, z których wyjechali rowerzyści, wynosi 60 km. Jak daleko przejedzie każdy rowerzysta, zanim się spotkają? (rozwiązanie pod zdjęciem)

Rozwiązanie:

• 12+8 = 20 (km/h) to łączna prędkość dwóch rowerzystów lub prędkość, z jaką się do siebie zbliżyli
• 60: 20 = 3 (h) to czas po jakim spotkali się kolarze
• 3 ⋅ 8 = 24 (km) to odległość przebyta przez pierwszego rowerzystę
• 12 ⋅ 3 = 36 (km) to odległość pokonana przez drugiego rowerzystę
• Sprawdź: 36+24=60 (km) to odległość pokonana przez dwóch rowerzystów.
• Odpowiedź: 24 km, 36 km.

Zaproponuj dzieciom rozwiązanie następujących zadań w formie gry. Może będą chcieli stworzyć swój własny problem o przyjaciołach, zwierzętach lub ptakach.

WIDEO: Problemy z poruszaniem się