Powierzchnia koła: formuła. Dlaczego obszar koła jest opisany i wpisany w kwadrat równy prostokątnemu trójkątowi równoramiennemu, prostokątnemu trapezowi równoramiennemu?

Jak znaleźć pole koła? Najpierw znajdź promień. Naucz się rozwiązywać proste i złożone zadania.

Okrąg jest krzywą zamkniętą. Każdy punkt na linii okręgu będzie w równej odległości od punktu środkowego. Okrąg ma kształt płaski, więc rozwiązanie zadania znalezienia obszaru jest proste. W tym artykule zastanowimy się, jak znaleźć obszar koła wpisanego w trójkąt, trapez, kwadrat i opisany w pobliżu tych figur.

Pole okręgu: wzór wykorzystujący promień, średnicę, długość okręgu, przykłady rozwiązywania problemów

Aby znaleźć pole liczba, musisz wiedzieć, że taki jest promień, średnica i liczba π.

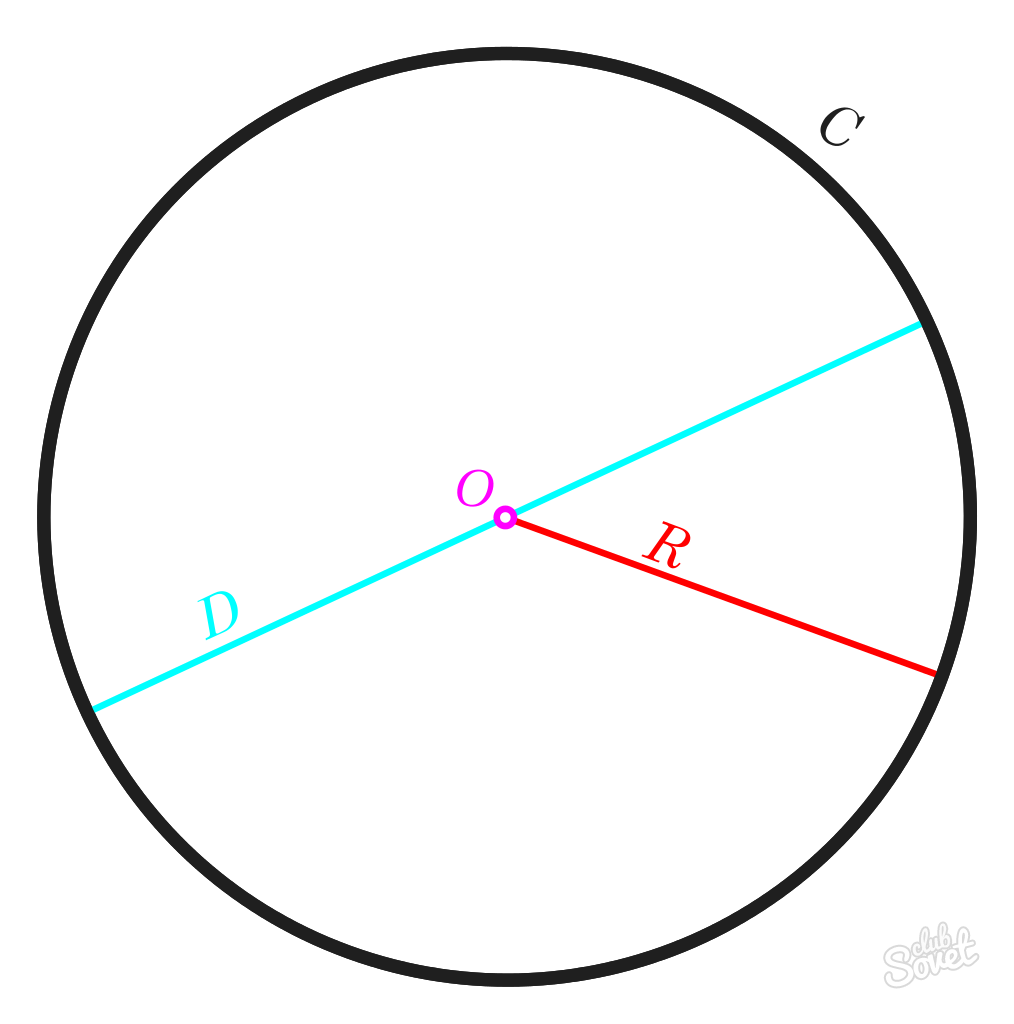
Promień R to odległość ograniczona przez środek okręgu. Długości wszystkich promieni R jednego okręgu będą równe.

Średnica D to linia pomiędzy dowolnymi dwoma punktami na okręgu przechodząca przez punkt środkowy. Długość tego segmentu jest równa długości promienia R pomnożonej przez 2.

Liczba π jest wartością stałą równą 3,1415926. W matematyce ta liczba jest zwykle zaokrąglana do 3,14.

Wzór na znalezienie pola koła przez promień:

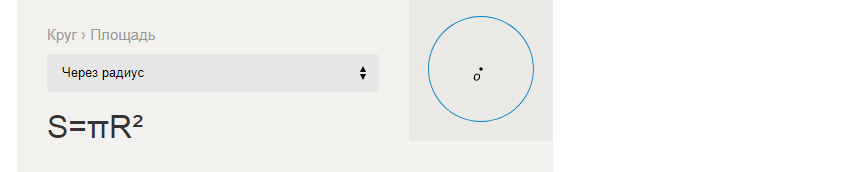
Przykłady rozwiązywania zadań do znalezienia pola S koła przez promień R:

---------- ---------------------------- --

Zadanie: Znajdź pole koła, jeśli jego promień wynosi 7 cm.

Rozwiązanie: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Odpowiedź: Powierzchnia koła to 153,86 cm2.

Wzór na znalezienie pola S koła przez średnicę D:

Przykłady rozwiązywania zadań na znalezienie S jeśli D jest znane:

--------- --------------------------------

Zadanie: Znajdź S okręgu, jeśli jego D jest równe 10 cm.

Rozwiązanie: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Odpowiedź: Powierzchnia płaskiej okrągłej figury wynosi 78,5 cm2.

Znalezienie S okręgu, jeśli długość okręgu jest znana:

Najpierw znajdujemy promień. Długość okręgu oblicza się ze wzoru: L=2πR, zatem promień R będzie równy L/2π. Teraz wyznaczamy pole koła za pomocą wzoru przez R.

Rozważmy rozwiązanie na przykładzie problemu:

----------- -----------------------------

Zadanie: Znajdź pole koła, jeśli znana jest długość koła L — 12 cm.

Rozwiązanie: Najpierw znajdujemy promień: R=L/2π=12/2*3,14=12/6,28=1,91.

Teraz znajdujemy obszar w promieniu: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Odpowiedź: Powierzchnia koła to 11,46 cm2.

Pole koła wpisanego w kwadrat: wzór, przykłady rozwiązywania zadań

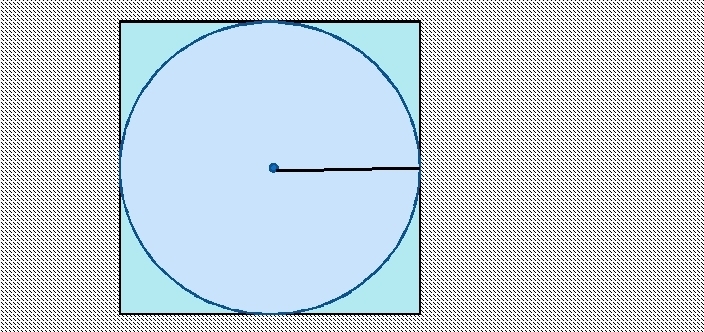
Znalezienie pola powierzchni koła wpisanego w kwadrat jest proste. Bok kwadratu to średnica koła. Aby znaleźć promień, musisz podzielić bok przez 2.

Wzór na znalezienie pola koła wpisanego w kwadrat:

Przykłady rozwiązywania problemów dotyczących znalezienia pola koła wpisanego w kwadrat kwadrat:

-- ---------------------------------- ----

Zadanie nr 1: Bok figury kwadratowej równy 6 centymetrom jest znany. Znajdź obszar S wpisanego koła.

Rozwiązanie: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Odpowiedź: Powierzchnia płaskiej okrągłej figury wynosi 28,26 cm2.

----------------------------------------- -----------

Zadanie #2 :Znajdź S okręgu wpisanego w kwadrat i jego promień, jeśli jeden bok jest równy a=4 patrz

Rozwiąż w następujący sposób : Najpierw znajdujemy R=a/2=4/2=2 patrz

Teraz znajdziemy pole koła S=3,14*22=3,14*4=12,56 cm2.

Odpowiedź: Powierzchnia płaskiej okrągłej figury wynosi 12,56 cm2.

Pole koła opisanego wokół kwadratu: wzór, przykłady rozwiązywania zadań

Trochę trudniej jest znaleźć pole figury okrągłej opisanej wokół kwadratu. Ale znając formułę, możesz szybko obliczyć tę wartość.

Wzór na znalezienie S koła opisanego wokół kwadratu:

Przykłady rozwiązywania problemów ze znalezieniem pola koła opisanego wokół figury kwadratowej:

Zadanie

Pole koła wpisanego w prawy trójkąt i równoramienny: wzór, przykłady rozwiązywania zadań

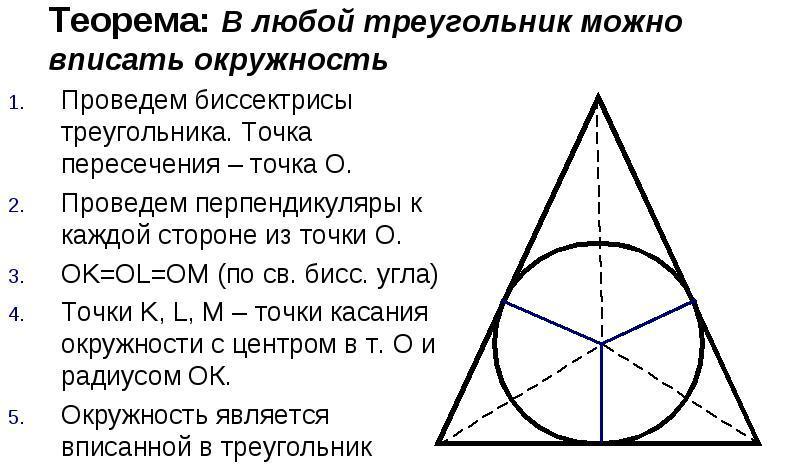
Okrąg wpisany w trójkąt to okrąg, który dotyka wszystkich trzech boków trójkąta. W okrąg można wpisać dowolną trójkątną figurę, ale tylko jedną. Środek okręgu będzie punktem przecięcia dwusiecznych kąta trójkąta.

Wzór na znalezienie pola koła wpisanego w trójkąt równoramienny:

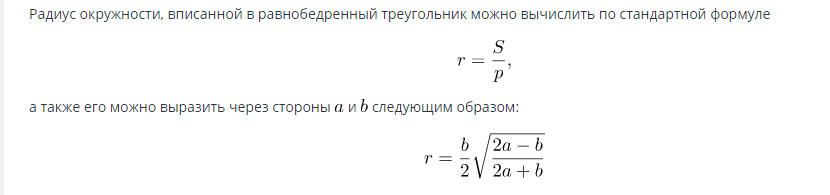
Znając promień, pole powierzchni można obliczyć ze wzoru: S=πR2.

Wzór na znalezienie pola koła wpisanego w trójkąt prostokątny:

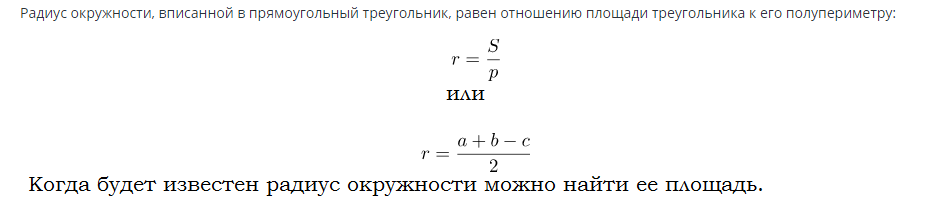
Przykłady rozwiązań problemów:

Zadanie # 1

)

Jeżeli w tym zadaniu trzeba również znaleźć pole koła o promieniu 4 cm, to można to zrobić ze wzoru: S=πR2

Zadanie #2

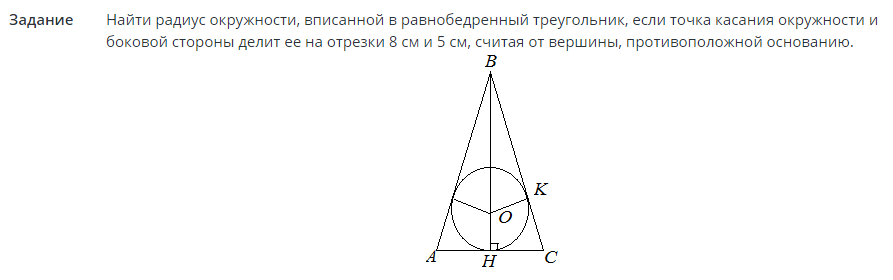
Rozwiązania:

Teraz, gdy promień jest znany, obszar koła można znaleźć pod względem promienia. Zobacz powyższy wzór w tekście.

Zadanie #3

Pole okręgu opisanego wokół trójkąta prostokątnego i równoramiennego: wzór, przykłady rozwiązywania zadań

Wszystkie wzory na znalezienie obszaru koła sprowadza się do tego, że najpierw musisz znaleźć jego promień. Gdy promień jest znany, znalezienie obszaru jest proste, jak opisano powyżej.

​​

Pole koła opisanego wokół trójkąta prostokątnego i równoramiennego określa wzór:

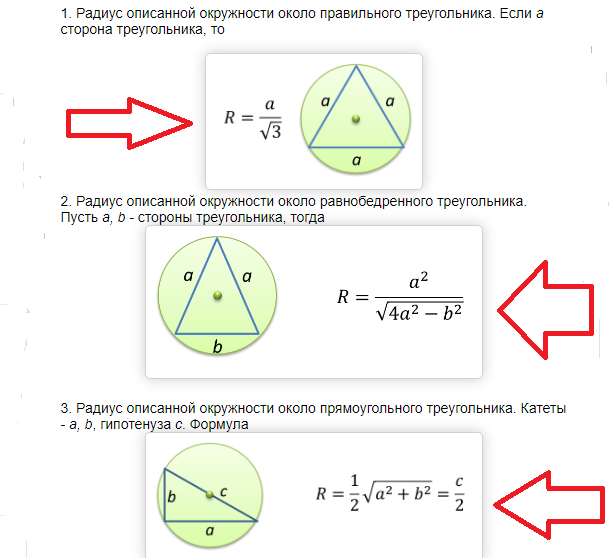
Przykłady rozwiązywania problemów:

Oto kolejny przykład rozwiązania problem przy użyciu wzoru Herona.

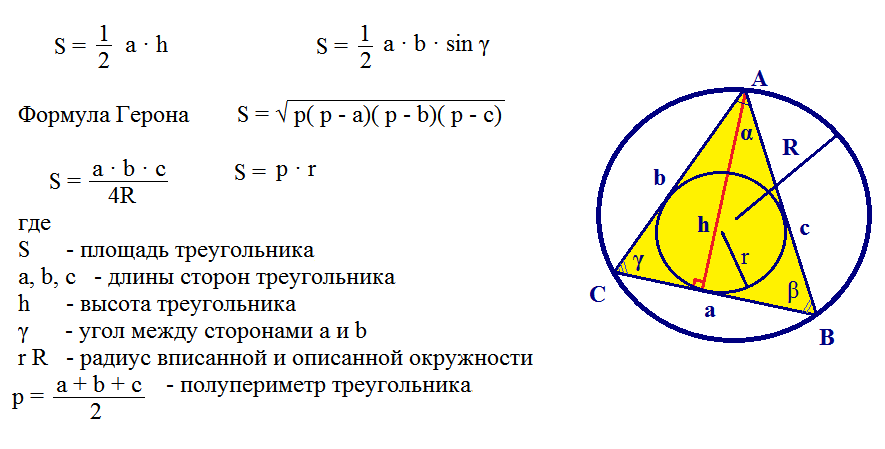
Trudne do rozwiązania podobne problemy, ale można je przezwyciężyć, jeśli znasz wszystkie formuły. Uczniowie rozwiązują takie zadania w 9 klasie.

Obszar koła wpisanego w prostokąt i trapez równoramienny: wzór, przykłady rozwiązywania problemów

Na przykład trapez równoramienny jest wpisany za pomocą okrąg znajdujący się w miejscu styku dzieli jedną stronę na odcinki m i n.

Aby rozwiązać ten problem, należy skorzystać z następujących wzorów:

Znalezienie pola koła wpisanego w prostokątny trapez odbywa się według wzoru:

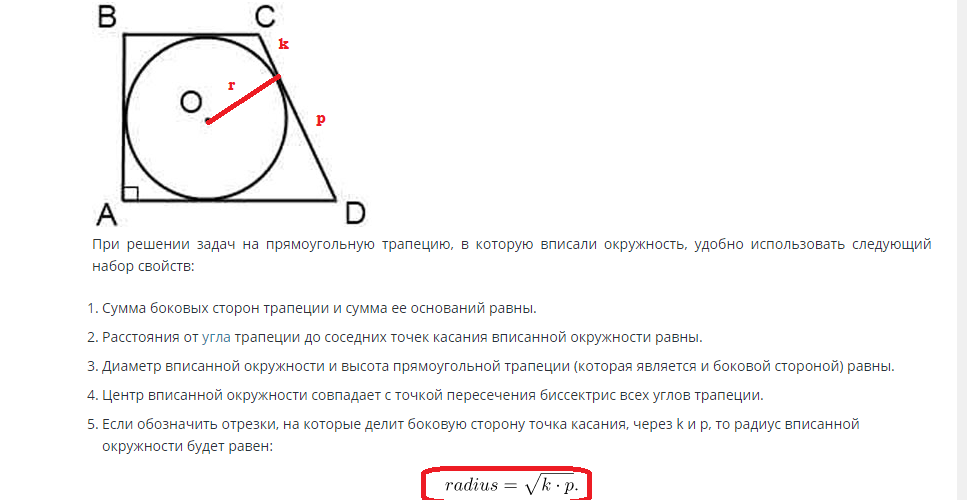
Jeśli znany jest bok, to promień można znaleźć przez tę wartość. Wysokość boku trapezu jest równa średnicy koła, a promień jest równy połowie średnicy. W związku z tym promień jest równy R=d/2.

Przykłady rozwiązywania zadań:

Pole koła opisanego wokół trapezu prostokątnego i równoramiennego: wzór, przykłady rozwiązywania problemów

Trapez można wpisać w kole, gdy suma przeciwnych kątów wynosi 180°. Dlatego można wpisać tylko trapez równoboczny. Promień do obliczenia pola koła opisanego w pobliżu trapezu prostokątnego lub równoramiennego oblicza się za pomocą następujących wzorów:

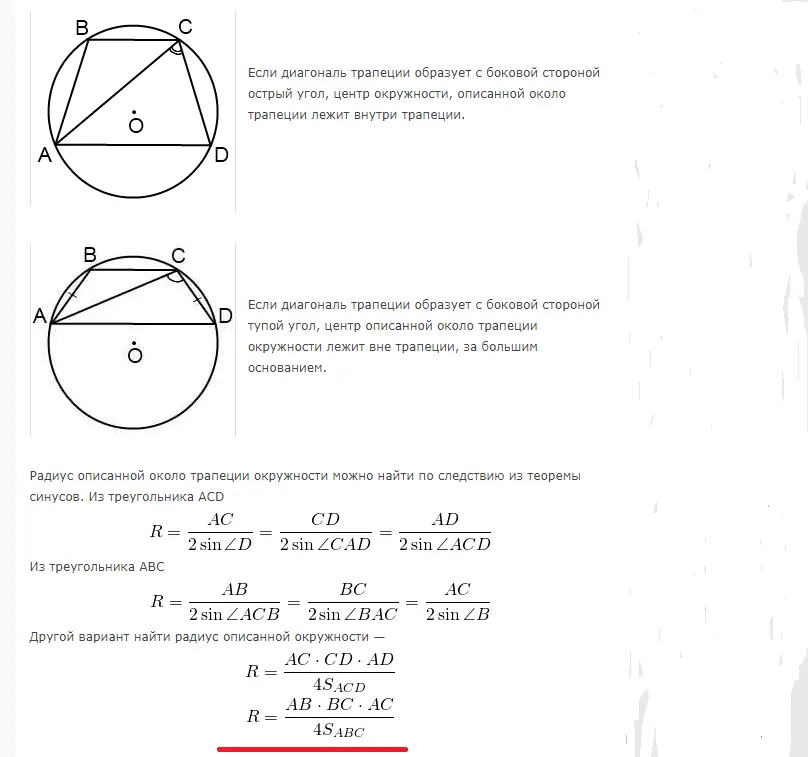
Przykłady rozwiązywania problemów:

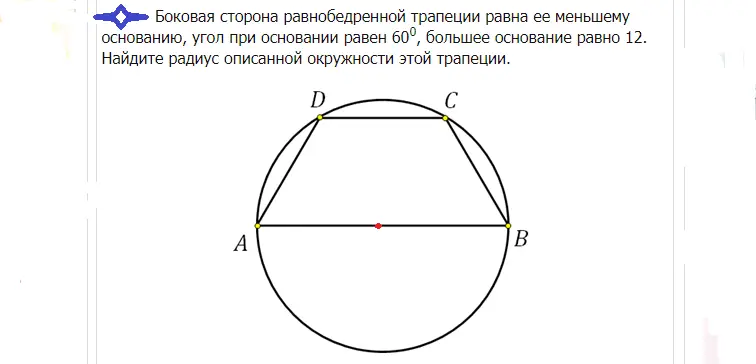
Rozwiązanie: Duża podstawa w tym przypadku przechodzi przez środek, ponieważ w okrąg wpisany jest trapez równoramienny. Centrum dzieli tę bazę dokładnie na pół. Jeżeli podstawa AB jest równa 12, to promień R można znaleźć następująco: R=12/2=6.

Odpowiedź: Promień wynosi 6.

W geometrii ważna jest znajomość wzorów. Ale nie można ich wszystkich zapamiętać, więc nawet na wielu egzaminach można używać specjalnego formularza. Jednak ważne jest, aby móc znaleźć odpowiednią formułę rozwiązania tego lub innego problemu. Ćwicz rozwiązywanie różnych problemów dotyczących znajdowania promienia i pola koła, aby móc poprawnie zastępować formuły i uzyskiwać dokładne odpowiedzi.

Wideo: Matematyka | Obliczanie pól koła i jego części